中华文教网移动版

     数学的发展有赖于数学创造性思维。在学生的学习过程中，虽然不一定能提出新的科学概念或发现新的理论，但所学知识对学生来讲都是首次遇到的，全新的。从这个意义上讲，学生通过对自身认知结构的完善，提出一些解决问题的新见解，新方法，得到未学的新知识，总结出有关规律，本身就是一种“再发现”式创造性思维活动。因此在教学中应着力培养学生的这种创造性思维，大力开展师生互动、畅所欲言、探究讨论的数学新局面。而回顾反思往往能整合、调整思维，产生许多“突闪的念头”或“顿悟”。
    一、反思解题途径，培养思维的多向性，独创性
    数学课堂教学中，解题教学是培养思维能力的重要形式，解题后的反思有助于学生对问题的深度挖掘。对问题多角度，多方位地思考可提高学生解决问题的灵活性和创新能力。而思维的独创性，是指在思维活动中能以独特的心理操作方式来展开思维，是思维成果新颖，与众不同的品质。解完一道题目之后，应思考根据此题要求解的结论能否从其它角度重新审视题目，条件相似时，会有相同的结果吗？条件不变时，还能得出其它结果吗？能否从所解题目出发编出一个属于自己的新题？沿着这些思路去反思，有助于培养思维的创造性。
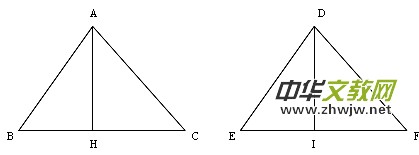
    例如：已知：如图△ABC≌△DEF，AH，DI分别是△ABC和△DEF的高。
求证：AH=DI例题分析证完后学生通过反思又提出了用三角形面积来证明的新思路，其证法简洁优美。

 

 

 ∵△ABC≌△DEF
 ∴S△ABC=S△DEF         B=EF
 ∴1/2BC·AH=1/2EF·DI
 ∴AH=DI
     “一石激起千层浪”奇妙的思维更激发了学生对问题的深度思考，在教师的指导下经过探讨归纳出了许多可用面积来证明的命题，如：
    等腰三角形两腰上的高相等。
    等腰三角形底边上中点到两腰的距离相等。
    等腰三角形底边两端到底边中线的距离相等。等腰三角形底边上的任意一点到两腰的距离和等于定值。
    二、反思题目特征，培养思维的深刻性
     在实施素质教育的今天，如何培养学生的思维品质，怎样提高学生分析问题和解决问题的能力，已成为一个值得认真研究和探讨的问题，现就其中的一个重要环节——解题后的反思作探讨，以求抛砖引玉。思维的深刻性表现在渗透表面现象和外部的联系，揭露事物的本质，进而深入思考问题。通过反思题目特征，加深对题目特征的本质领悟，从而获得一系列的思维成果。理解题意就是从题目中获取达到解题目标的信息，反思理解题意过程就是对如何获取信息的思考。如获得了哪些信息，漏掉了哪些信息。为什么会漏掉这些信息，导致解答错误或繁杂等。数学学习活动中，经常对问题特征进行放缩，特殊化，推广等变式探究，有助于培养思维的深刻性。
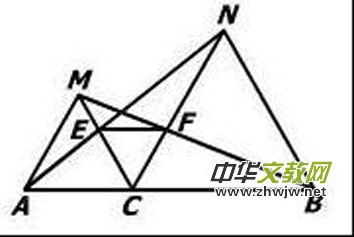
    例如：已知：如图，点C为线段AB上一点，△ACM，△CBN是等边三角形。
     求证：AN=BM

   

 
    反思题目特征可作出如下思考：
    （1）△CBN固定，将△ACM绕C旋转一定角度后，结论有何变化？
    （2）若点C不在AB上，则为：△ABC，以AC，BC 为边向外作等边三角形△ACM，△BCN，连结AN，BM，结论是否成立？
    （3）在原题中若CM与AN交于E，BM与CN交于F，试判断△CEF的形状。
    三、反思数学思想方法，培养思维的流畅性
    数学教学不应只是数学知识的教学，还应包括数学思想方法的教学，它是数学的灵魂，在数学中重视数学思想方法，有助于思维能力的流畅，有利于创造能力的发展。
    例如：已知： 
    从数学思想方法上反思是用了化归，降次。因此，学生经过思考便解决了类似 这样的方程。尝试并成功解决了 等方程。极大地调动了学生的学习积极性，主动性。
    四、反思解题的正确性，培养学生思维的严谨性
    解题中往往受思维定势或粗心大意等因素的影响，导致解答不正确。因此在解题后需要对解题的正确性进行反思，以培养思维的严谨性。解数学题时往往有这么一种现象，对一些含有附加条件的问题，虽然简单易解，但是学生没有认真审题，未能充分考虑条件中隐含的深层含义，无法读取完整信息而造成解题失误。
    例如：如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度为9米）围成一个中间隔有一道篱笆的长方形养鸡场。设养鸡场的长BC为X米，面积为S平方米。

 

 

     ①求S与X的函数关系式
     ②当长方形的长为多少时，养鸡场的面积最大，最大面积是多少？
    此题易求出S与的函数关系式 ，根据“二次项系数a＜0，当  时，二次函数S有最大值”得：当=12时，S有最大值48。但此时研究实际问题中的函数关系，没有考虑到定义域，忽略了附加条件“墙的最大可用长度为9米”，即在自变量的取值范围内取不到X=12。所以正确的解答是要结合图像，从函数值变化的角度，才能确认当长方形的长最大值为9米时，养鸡场的面积最大为45平方米。
    总之，学生进行解题后反思，能培养学生思维品质。在新课改数学教学中，教师注意引导学生解题反思能优化学生思维的多向性、独创性、深刻性、流畅性、严谨性。让学生学会反思，从中受益，学生就会愿意反思，经过反思，促进学生的思维升华到一个更高的水平，使学生获得深入学习所必需的思维品质，“授之以渔”，“让学生主动发展”，真正体现“以学生发展为本”的教育理念。
    （作者单位：梅州市五华县油田中学）