中华文教网移动版

       辅助线是图形转化的桥梁，也是学习几何的一个特点，添加辅助线是我们在证明和解几何题经常采用的方法，如果运用恰当，就会起到事半功倍的效果，那么如何让它起到桥梁的作用呢？下面以四边形中添加辅助线为例加以说明。
       一、连接点
       例1：如图1所示，在矩形ABCD中，AB=3,AD=4,P在AD上的动点，PE⊥AD于点E,PE⊥AD于F,则PE+PF的值为__________PD

 
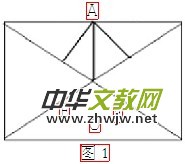
       分析：连接OP，利用S△=S△AOP+S△DOP解答问题，因为四边形ABCD是矩形，且AB=3,AD=4,由勾股定理的AC=BD=5。
       因为对角线互相平分
 OA=OD=5/2因为PE⊥AC,PE⊥BD,所以S△AOD=S△AOP+S△DOP=1/2AO·PE+1/2DO·PF=5/4(PE+PF)。
     又因为在矩形ABCD中，S△AOD=1/2S△ABD=1/2×1/2×3×4=3,所以5/4(PE+PF)=3,解得PE+PF=12/5
       解：填12/5
       二、有中点构造中位线
       例2：如图2，AE为正方形ABCD中∠BAC的平分线，AE分别交BD于F,交BC于点E,AC和BD相交于O。
求证：OF=1/2CE

 
       分析：欲证OF=1/2CE,根据图形特点，关键是找一条于OF相等又与CE有密切关系的线段，考虑到O是AC的中点，故取AE的中点，作△AEC的中位线，利用中位线的性质可使问题得以解决。
       证明：取AE的中点，连接ON,可得ON为△AEC的中位线所以ON∥CE,ON=1/2CE,所以∠6=∠ONE
       因为四边形ABCD是正方形，所以∠3=∠4=45°又∠5=∠1+∠3，∠6=∠2+∠4而∠1=∠2，所以∠5=∠6故∠5=∠ONE，所以ON=OF从而可得OF=1/2CE
       三、连接菱形对角线
       例3：如图3，在菱形ABCD中，E、F分别是BC、CD上的点，∠B=∠EAF=60°,∠BAE=18°，求∠CEF的度数。

 
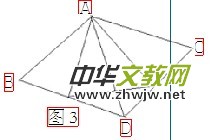
       分析：本题考查菱形的性质和等边三角形的性质及判定，连接AC,可得△ABC为正三角形，易得∠BAE=∠CAF，△BAE≌△CAF，进而推出△AEF为等边三角形，则∠CEF的度数即可求得。
       解：连接AC,在菱形ABCD中，可得BA=BC
       因为∠B=60°,所以△ABC、△ACD为正三角形所以∠BAC=∠ACB=60°,AB=AC又因为∠EAF=∠BAC=600,所以∠BAE=∠CAF又因为∠B=∠ACF=60°，AB=AC，所以△BAE≌△CAF所以△AEF是等边三角形又由∠AEC=∠B+∠BAE=78°可得∠CEF=∠AEC-∠AEF=78°-60°=18°
       四、平移梯形对角线
       例4：如图4在梯形ABCD中，AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则梯形的中位线长是（     ）
A、 10     B、 6      C、 15/2        D、12

 
       分析：梯形问题中，遇到对角线垂直，可平移对角线，将梯形问题转化为平行四边形和特殊的三角形问题后，再运用相关的性质解题A
     做DE∥AC交BC的延长线于点E，则四边形ACED是平行四边形，所以
DE=AC=12,AD=CE
       因为AC⊥BD,所以BD⊥DE
      在Rt△BDE中，∠BDE=900,BD=9,DE=12,AD=AE,所以
     BE=BD+DE=92+122=81=144=225
       解得BE=15.
      故梯形的中位线长=1/2（AD+BC）=1/2
       (CE+BC)=1/2BE=1/2×15=15/2
       解：选Ｃ
       总结：解决四边形问题，常通过添加辅助线转化为三角形问题来解决，以上是解决四边形问题常用辅助线做法，通过作辅助线可以化难为易，化繁为简，从而找到解决问题的途径。
    （作者单位：云南省永胜县永北镇中学）