中华文教网移动版

中学数学创新思维能力的培养

          中央民族大学附属中学     廖海峰

    【内容提要】

创新始于问题，在中学数学教学过程中实施创新教育，要遵偱发现数学问题的规律，引导学生运用归纳猜想、类比猜想和逆向思维等思维方式来发现数学问题，从而执着地探索解决问题，使学生感受到创新过程带来的“快乐”体验，进一步地激励学生再发现和再创造，形成一种良性机制，对学生的教育意义极其重大。

    【主题词】

数学创新教育  发现问题   归纳猜想  类比猜想  逆向思维

     【正文】

    “创新”一词就是创立或创造新的东西的意思，创新教育就是指培养人的创新精神和创新能力的教育，是指通过对学生施以教育和影响，以扎实的基础知识、熟练的基本技能和一定的思维能力为基础，使他们能够发现和认识有意义的新知识、新思想、新事物、新方法。中学数学教学中实施创新教育，就是根据学生的具体情况及数学知识本身的内在规律，通过数学教学活动，使他们具有发现并解决数学问题的能力。

二十一世纪人才的培养是创新人才的培养，而创新人才的培养离不开创新教育。随着社会的发展，作为素质教育重要内容的“创新教育”已成为人们关注的热点。在数学教学中重视创新教育，培养学生的创新思维能力是时代对数学教育提出的新要求。在新课程的标准下中学数学教学中如何培养中学生的创新能力，这是我们教师所面临的一个新的挑战。

创新始于问题，爱因斯坦强调：“发现问题和系统阐述问题可能要比得到解答更为重要，解答可能仅仅是数学或实验技能问题。”所以在中学数学教学过程中实施创新教育，首先是要创建恰当的情境，引导学生发现问题、提出问题，然后才是让学生主动地分析、解决问题。根据数学学科的特点，问题的发现是有规律可偱的。在中学阶段可运用归纳猜想、类比猜想和逆向思维等思维方式来发现数学问题。

下面用一个案例来谈谈在实际中学数学教学过程中，如何引导学生运用类比猜想、归纳猜想和逆向思维来发现问题，培养学生数学创新思维能力。这个案例是从类比猜想提出问题开始，到最后问题的解决经历了近两年的时间，经历了非常曲折的过程。

我在高一给学生复习反比例函数时，学生在初中就知道其图像为双曲线，有两条渐近线。后来讲到函数时，其图像形状与双曲线相似，也有两条渐近线，于是就引导学生运用类比猜想，提出这样的问题：函数的图像是否双曲线？由于高一的学生还没有学习圆锥曲线，所以我告诉学生，要等到高二系统学习了双曲线后才能解决这个问题，于是就将这个问题暂时搁置下来。

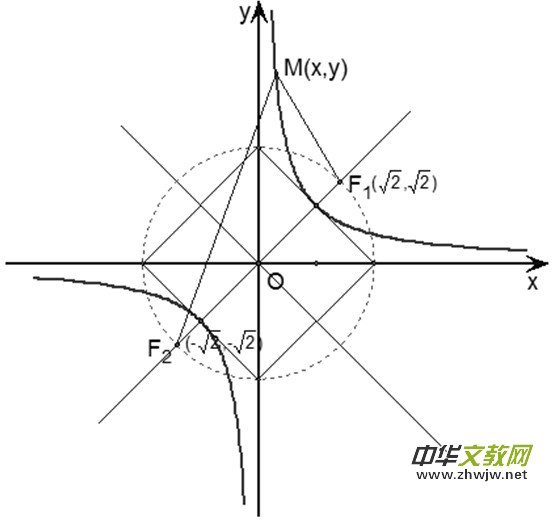
等到在高二给学生讲双曲线时，利用双曲线的性质，找到双曲线的对称轴，从而找到双曲线的焦点，设双曲线上的任意动点，可证明动点满足：，符合双曲线的定义，也就说明函数的图像为双曲线。学生自然地也试图运用双曲线的定义来证明函数的图像也是双曲线，但是有很大的困难，因为不好确定双曲线的焦点坐标，所以利用双曲线的定义来证明函数的图像是双曲线没有成功。

观察函数的图像易知：过图像上任意点分别作两渐近线的平行线，两平行线分别与两渐近线交于两点，四边形的面积为定值。

后来通过《几何画板》研究双曲线时，也得到双曲线也有相同的性质：过双曲线上任意点分别作两渐近线的平行线，两平行线分别与两渐近线交于两点，四边形的面积为定值。

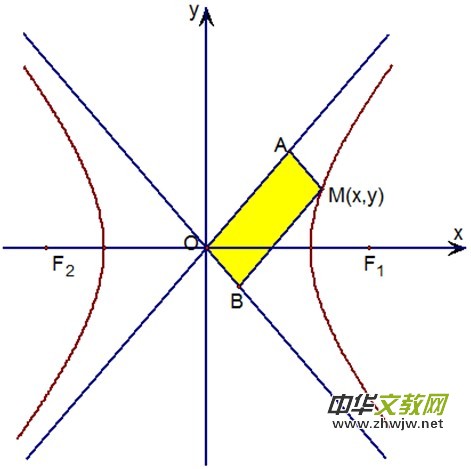
学生很自然地运用归纳猜想，得到双曲线有如下性质：过双曲线上任意一点分别作渐近线的平行线，与两渐近线的交点为，则平行四边形的面积为定值。学生通过证明，发现这个定值为。

学生运用逆向思维，大胆地提出了这样一个问题：过动点分别作两直线的平行线，与这两直线分别交于两点，若平行四边形的面积为定值，动点的轨迹是否为双曲线？

对于学生提出的这个问题，我马上给予了肯定，这个问题同时也引起了同学们的极大的兴趣。学生运用刚学的解析几何中曲线与方程的思想，发现只要求出了动点的轨迹方程，就能解决这个问题。学生运用所学的轨迹方程的求法，求动点的轨迹方程：

已知直线，，，

联立得点，

，

点到直线的距离为，

所以四边形的面积

，

而，所以有，

从而得到动点的方程为，表明动点轨迹为互为共轭的双曲线，以上结论表明：我们可以从另一个角度来定义双曲线。

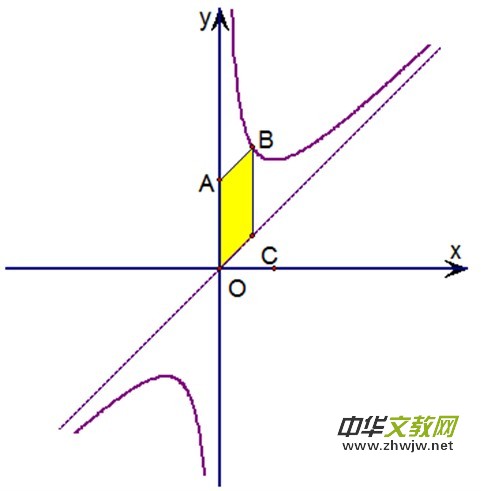
最后让我没有想到的是，学生将高一没有解决的问题，又重新提了出来：函数的图像是否双曲线？并根据以上的结论，并提出可以运用以上结论来证明函数的图像是双曲线：要证函数的图像是双曲线，即证如图所示平行四边形的面积为定值即可。学生证明如下：

令，所以，得到平行四边形的面积，因此证明了函数的图像是双曲线，同理易证函数的图像也是双曲线，且与函数的图像是互为共轭的双曲线。

通过以上问题的解决过程，使我感触很深，学生从类比猜想得到的问题开始，在历时近两年的时间内，一直保持着强烈的“好奇”与“质疑”，在执着地探索问题的解决，从而激发了学生一连串的思考，引起学生强烈的探索欲望，最终解决了提出的问题，这实际上就是一次完整创新体验活动。而这种创新体验活动，给学生带来了“快乐”的体验，进一步地激励学生再发现和再创造，形成一种良性机制，对学生的教育意义是极其重大的。

问题是思维的动力，是创新精神的基石。培养创新精神，应始于问题意识。然而问题意识不是天生的，它也需要培养和激发。所以在数学教育中实施素质教育，就是要对学生进行创新教育，要引导学生学会运用归纳猜想、类比猜想和逆向思维等思维方式来发现数学问题，从而引起学生执着地探索解决问题，可以让学生体会到发现的乐趣，从而激励再发现和再创新，在数学领域培养更多的创新型人才。

   【参考文献】

青岛大学师范学院学报《强化问题意识，培养创新人才》作者：李明兰