中华文教网移动版

                    巧制教具，活教《圆》

湖北省老河口市第三中学 童建林

数学教学中如果借助多媒体进行辅助，固然十分重要。然而在实际教学中，由于各地方条件不同不可能每间教室都配备有多媒体，何况也不可能都能根据需要制作课件，因此笔者认为教师可以根据教学需要自制教具。九年级《圆》这章内容笔者在教学中制作了大量的教具进行辅助教学实验，效果十分明显。下面举些例子进行说明。

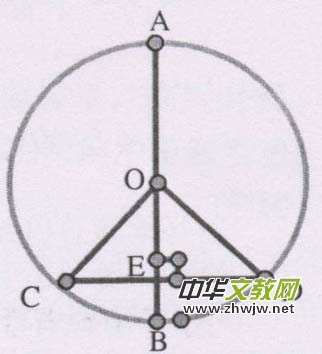
1、在垂经定理第一节课我用纸板制作了个圆如右图，将圆折叠学生很容易得出圆的轴对称性，若AB⊥CD然后沿直经AB折叠让学生观察点C和点D重合，CE=DE，弧 BC =弧BD ，弧 AC=弧AD，学生比较直观感受到垂经定理同时为学习本节课垂经定理的应用节省了时间。

2、在弧、弦、圆心角的第一节课我制作了个纸扇，让学生观察这个纸扇合起来时，其圆心角相等，圆心角所对弧、弦（指同一个圆）实际也重合从而提出本节课内容，极大的激发了学生学习兴趣，同时对本节内容也有了初步的感知，在学习过程中还可以借助纸扇的内外两个扇形体会弧、弦、圆心角关系定理成立条件是同圆或者等圆。

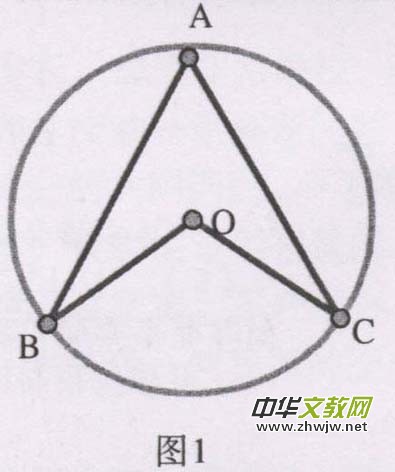
 3、在学习圆周角定理第一节课中圆周角定理的三种情况分类证明是个难点我制作了如右图1的教具，用了一个皮筋代表AB和AC，点B，C固定皮筋两端，点A绕着圆周移动这样就很直观的把圆周角与圆心三种位置关系即圆心在圆周角的外部，内部，一条边上展现给学生，难点得以突破。

4、在学习与圆有关的位置关系中我制作了一个教具如右图2，

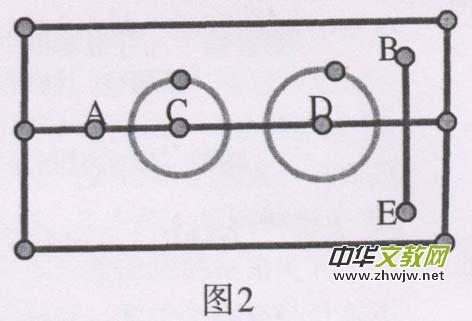
在一个硬纸板中间拉一条细铁丝将纸板做成的点A，圆C，和圆D，以及直线BE穿在上面，通过移动点可以得到点与圆的三种位置关系以及对应的数量，移动圆C和圆D得到圆与圆5种位置关系，通过移动直线BE可以得到线与圆的3种位置以及对应的数量关系等， 这样就可以使课本的内容“动”起来，学生很容易掌握，而且经济适用大家都可以做，我在通过自制教具教学过程中，我的同事都做起了教具。当然圆这一章还有许多内容可以自制教具比如圆锥，圆柱体的侧面展开图等。

总之，通过自制教具进行数学教学，可以使课堂活起来，教学内容“动” 起来，学生学习乐起来，教育教学质量高起来。