中华文教网移动版

 

       【文摘】探索具体问题中的数量关系和变化规律，采用从特殊到一般、数形结合的重要数学思想方法，培养学生的探究创新能力。
       【关键词】规律性问题、数列找规律、算式找规律、“数形结合”的数学方法找规律
        新课程标准中明确提出：“探索具体问题中的数量关系和变化规律”。数学中的规律性问题是指在一定条件下，探索发现有关数学对象所具有的规律性或不变性的问题。规律性问题的特点是问题的结论或条件不直接给出，而常常是给出了一列数、一列等式、一列图形的前几个，要求学生通过阅读、观察、分析、综合、归纳、概括、判断等一系列探索活动逐步确定需求的结论或条件。它体现了从“特殊到一般”的数学思想方法，解决探索规律性问题，让学生经历观察、比较、归纳猜想的过程，从而培养学生的探究创新能力。初中数学规律性问题可分为数与式、平面图形与立体图形问题。通过课堂实录我总结了以下几种解决规律性问题的方法，以供各位同仁参考，同时更希望起到抛砖引玉的功效。
       一、利用数列找规律
     （一）等差数列：定义：一般地如果一列数列从第二项起每一项与它的前一项的差都等于同一个常数，那么这个数列就叫做等差数列。这个常数叫做等差数列的公差。常用字母d表示。
       1、增幅相等：对每个数和它的前一个数进行比较，如增幅相等，则第n个数可以表示为：a+(n-1)d，其中a为数列的第一位数，d为增幅，(n-1)d为第一位数到第n位的总增幅。然后再简化代数式a+(n-1)d。例：4、10、16、22、28……求第n位数。
       分析：第二位数起，每位数都比前一位数增加6，增幅相都是6，所以，第n位数是：4+(n-1)×6＝6n－2
       2、增幅不相等，但是，增幅以同等幅度增加（即增幅的增幅相等，也即增幅为等差数列）。如增幅分别为3、5、7、9，说明增幅以同等幅度增加。此种数列第n位的数也有一种通用求法。
       基本思路是：1、求出数列的第n-1位到第n位的增幅；2、求出第1位到第n位的总增幅；3、数列的第1位数加上总增幅即是第n位数。
       举例说明：2、5、10、17……求第n位数。
       分析：数列的增幅分别为：3、5、7增幅以同等幅度增加。那么，数列的第n-1位到第n位的增幅是：3+2×(n-2)=2n-1，总增幅为：【3+（2n-1）】×(n-1)÷2＝（n+1）×(n2-1)＝n2-  1，所以第n位数是：2+ n2-1= n2+1
       此解法虽然较烦，但是此类题的通用解法，当然此题也可用其它技巧，或用分析观察凑的方法求出，方法就简单的多了。
      （二）等比数列：定义：如果一列数列从第二项起，每一项与它的前一项的比等于同一个常数，这个数列叫做等比数列。这个常数叫做等比数列的公比.用字母q表示。如2、4、8、16……求第n位数
       分析：数列中的每一个数（从第二个开始）与前一个数的比是2，所以数列的第n位数是：2x2n-1 公式：a n=a1×q n-1 。
       例1 观察下面的一列单项式：-x，2x2,-4x3，8x4，-16x5…,根据其中的规律得出第10个单项式是：（  ）
     （A）-29x10     (B)29x10        (C)-29x9       (D)29X9
      (解析)选B。依题意得：（1）n为奇数，单项式为：-2n-1xn；（2）n为偶数时，单项式为：2n-1·（-x）n,第10个单项式为29x10.故选B。
       二、根据算式找规律
根据算式找规律就是从每个算式的自身特点，以及前后算式之间的联系发现、总结规律。
例2已知：A23=3×2=6, A35=5×4×3=60,A49=9×8×7×6=3024观察前面的计算规律计算A213=—（直接写出结果），并比较A47—A36（填﹥或﹤或=）
（解析）A47=7×6×5×4=840    A36=8×7×6=336，所以A47﹥ A36
       三、利用“数形结合”的数学方法找规律
     “数形结合”是数学教学中最重要的思想方法之一。华罗庚先生曾指出：“数缺性时少直观，形少数时难入微；数形结合百般好，隔裂分家万事非”，将其特点直观、形象、快捷阐述得淋漓尽致。“数形结合”作为一种数学思想方法,它的应用大致分为两种情形：或借助于数的精确性来阐明形的某些属性；或者借助于形的几何直观性来阐明数之间的某种关系。使复杂的问题简单化，抽象的问题具体化，化难为易，快速准确发现规律。
       例3：如图是用三角形摆成的图案，摆第1层图需要1个三角形，摆第2层图需要3个三角形，摆第3层图需要7个三角形，摆第4层图需要13个三角形，摆第5层图需要——个三角形，摆第n层图需要——个三角形
                   
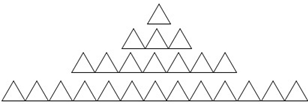
       由图观察可知摆第1层图需要1个三角形；摆第2层图需要22-2+1=3个三角形；摆第3层图需要32-3+1=7个三角形；摆第4层图需要42-4+1=13个三角形；摆第5层图需要52-5+1=21个三角形……那么摆第n层图需要n2-n+1个三角形。
　　例4：由n个相同的小正方形堆成的几何体，七视图如下所示，则n的最大值是（  ）
                            
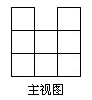
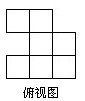
        A.18            B.19               C.20             D.21
       根据主视图和俯视图的关系可知通过主视图将正方形每根可达的最大值标注在俯视图上，如图即n的最大值为6+6+6=18     即选A
                
                                                （作者：贵州省凤冈县天桥中学）